Is it possible for money to generate more money and grow independently over time?

The answer is an absolute yes and it relies heavily on the Compound Interest concept. As I will be showing throughout my Posts, Compound Interest will be a Central and Basic Tool to help me quantify the attractiveness of different options and hence support my financial logic and my decision making process. I need to set the path clear for the future so that my money mindset can be better understood. In this sense, this post is written with the intention to fill that gap and bring some light into commonly used but not often fully understood financial questions and terms.

What are Interest Rates?

When it comes to saving, there are three avenues we can take:

• Keep the money stashed away. For example: in a current bank account or under the mattress.
• Place it in a savings account. For example: in a Cash ISA Account.
• Invest it. For example: in stocks and shares.

The pure fact that we are ruling out the opportunity of using that money immediately means that we must reasonably expect a reward for not doing so. That reward is proportional to the risk of losing part or all of that money when placed in the desired vehicle:

• Current account. Very Low/No risk –> No Reward
• Cash ISA. Low Risk –> Low Reward
• Stocks & Shares. Medium/High Risk –> Medium to High Rewards

On this basis, we can now stablish that the Reward has two components attached: a) we are not making use of that money and, b) we are risking it in order to obtain a return.

That reward is called the Interest Rate and is expressed as a percentage.

The third component to complete the full picture is time as interest rates are time-bound. To illustrate it with an example: if I place £10,000 in a savings account offering an interest rate of 5% after a year, at the end of the year, I will get paid a £500 reward (5% of £10,000) for not having made use of that money making it a grand total of £10,500 in my savings account. However, if the interest rate offered was 5% payable after a month, I will end up with a £6,000 reward at the end of the year. A significantly different reward scenario.

Let me emphasize the time element when it comes to money as it is often overlooked or misunderstood. The previous example is revealing. What we are actually saying is that £10,000 is the same amount of money as £10,500. What is making these figures equal is a time difference of a year. In other words, it will be the same having £10,000 now than £10,500 in a year in money terms.

What is Compound Interest?

Going back the previous example, if at the end of the first year I decided to commit my £10,000 for another year, I would end up with £11,000 at the end of that second year. In this scenario, the return is based only on the initial sum of £10,000 regardless of the reward accrued. This type of interest is called Simple Interest Rate.

Compound Interest work very differently. In a compounding scenario, the interest reward will generate interest rewards as well. So the £500 at the end of the first year will equate to £525 at the end of the second year and the total amount of money after two years will be £11,525. In summary, at the end of the first year, I will have £10,500 (the initial sum of £10,000 plus the £500 interest reward), and at the end of the second year I will have £11,025: the new ‘initial sum’ of £10,500 plus £525 interest.

How much money will we accrue if we decided to keep it invested for 5 years? If we break down the interest reward year on year and compounded it, we will end up with the following figures:

End of Year 1: £500

EOY 2: £525

EOY 3: £551

EOY 4: £579

EOY 5: £609

That is to say that £500 will grow into £609 after four years. If we add all the interest returns, we will end up with £12,764 after five years. Not bad at all.

Some interesting facts:

What figure can we expect after 10 years? £16,290

How long will it take for my initial investment to double? £19,800 after 14 years.

It will take 22 years to Triple and 28 years to Quadruple.

So, if for instance you bought your house for £100,000 at some point in time, and assuming a 5% price increase year on year, you can expect your home to triple in value after approximately 20 years. 

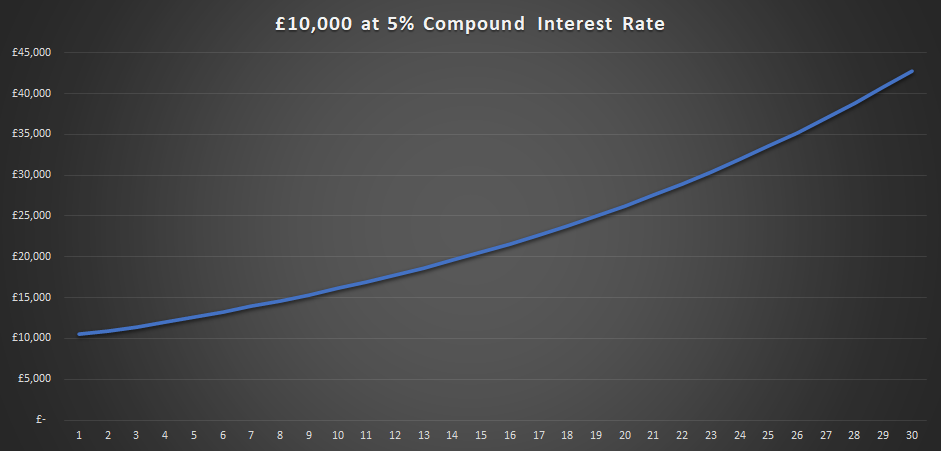
Compound interest grows exponentially and not proportionally. That means, that the sooner you invest and the longest you keep your investment for, the higher the growth.

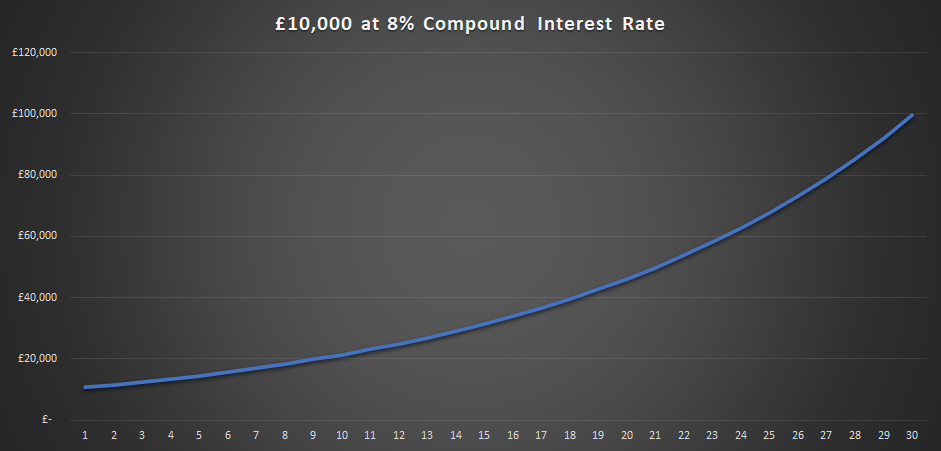
What if the compound interest rate is 8%? You will double your money after 10 years and triple it after 14. You will accrue £50,000 after 21 years and £100,000 after 30 years.

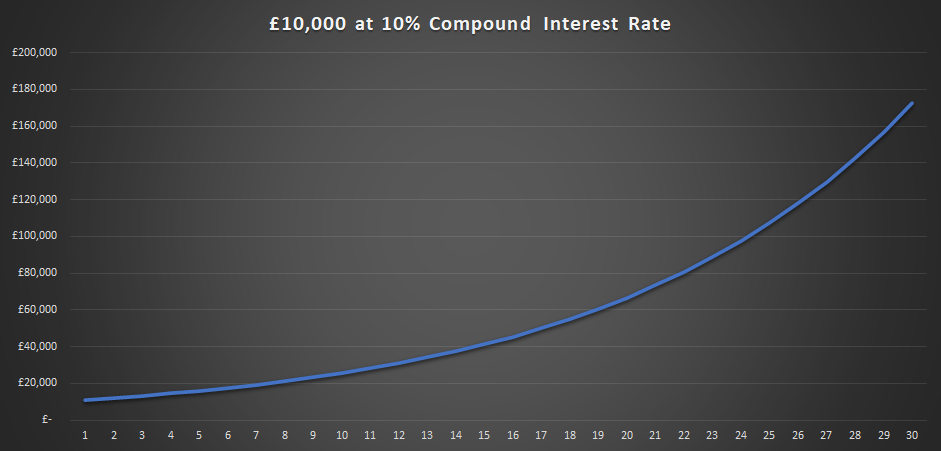
You will double your money in 7 years at a 10% Compound Interest Rate.

Rough compound interest calculation rule of thumb : Divide 72 by the annual interest rate and that’s approximately how long it takes debts to double, so 72 divided by 9% equals eight years.

These figures are almost magic. That is why Albert Einstein was quoted as calling it the eighth wonder of the world or man’s greatest invention. I could not agree more. I would add that compound interest rates are the shortest path to wealth. Stock Market traders are able to shorten the time span for these returns from years to months as they compound their profits several times over the course of a year.

What is Inflation?

An academic definition is that inflation is the reduction of purchasing power of money over time. What in reality means is that money loses value as time goes by when it comes to medium of exchange for goods and services. Inflation is a representation of the fact that prices increase over time whereas face value of money remains the same.

Inflation is measured as a percentage and is normally calculated over an annual period. For example, an inflation rate of 3% will mean that we will need £1,030 pounds worth of money one year into the future to purchase the same basket of goods and services that we can today buy for £1,000.

Inflation can be explained in terms of Compound Interest. It sets the bar for the minimum return in order to main Wealth and/or not experience a loss of personal Net Value. As an example: if inflation rate is 3%, I will need all my assets, income and money to increase equally just to keep my Personal Net Value intact relative to the purchasing power of money. Otherwise, I will become poorer. Let’s use some figures based on £1,000 lump sum and a 3% inflation rate.

I will need £1,030 in one year’s time to purchase the same basket of goods and services I can purchase today for £1,000. An alternative stand point is that £1,000 today will be worth £971 in a year’s time. Both of them quantify inflation over a year, the difference is the point in time chosen to measure (today or one year into the future).

Needed: £1,061 / worth: £943 in two year’s time.

£1,093 / £915 in three years.

£1,125 / £888 in four years.

£1,159 / £863 in five years.

It is absolutely paramount to understand that this is far more than a maths exercise. From an investment point of view, it is critical to understand inflation and compound interest rates. We will be in a position to make informed decisions as well as answer relevant questions as the ones I present below:

1. Which one of the two options is best: getting paid a £1,000 a year for the next 5 years or getting paid today £4,750?
2. If I deposit my money on a savings account at 1% per year, am I actually earning or losing money?
3. Given the same interest, which option is going to deliver best returns after 5 years: invest £5,000 pounds today or invest £1,000 every year?

I will not be answering them just yet. I will let you dwell on them for a while.

Why is inflation important when it comes to Saving and Investing?

If you have read thus far and followed my reasoning, why inflation must be considered before saving or investing money should be clear by now. Allow me be blunt though: any investment proposition or savings account return below inflation will make you lose money. Period.

Let me exemplify by answer question number 2.

After one year, £1,000 in a savings account at 1% will translate into £1,010. Looks like I am earning so far. However, at a 3% inflation rate, I will need £1,030 to buy the same basket of goods and services as a year in the past. Net result is a £20 loss.

The sad news is that the loss will grow exponentially over the course of several years. That is fact. Numbers do not lie. In my book, and as a bare minimum, returns must match o surpass inflation for any investment or saving proposition if I am intending to increase my personal Net Value.

The Dark Side of Compound Interest – Compounded Debt

If you happen to be in a situation where your debt is compounded, you definitely need to act to get out of it. Fast. Let me illustrate my point by means of a practical example:

Credit Card Debt: £1,000

APR: 20% Equivalent to a compounded monthly interest rate of 1.67%

If no payment is made to clear the debt, it will rise up to £1,220 after the first year. Times that by the thousand you owe.

Month	Debt
1	£          1,017
2	£          1,034
3	£          1,051
4	£          1,068
5	£          1,086
6	£          1,104
7	£          1,123
8	£          1,142
9	£          1,161
10	£          1,180
11	£          1,200
12	£          1,220

Let’s say that you owe £10,000 in credit card debt and that you make minimum payments of 1% of the outstanding balance every month:

Month	Debt	Interest charged	Minimum Payment
1	£        10,000	£              167	£              100
2	£        10,067	£              168	£              101
3	£        10,134	£              169	£              101
4	£        10,202	£              170	£              102
5	£        10,271	£              172	£              103
6	£        10,340	£              173	£              103
7	£        10,409	£              174	£              104
8	£        10,479	£              175	£              105
9	£        10,549	£              176	£              105
10	£        10,619	£              177	£              106
11	£        10,691	£              179	£              107
12	£        10,762	£              180	£              108

The debt interest on the credit card will be charged and added to your outstanding balance on a monthly basis. The minimum payment of 1% will not cover the interest charge. The debt will snowball (0.67% compounded monthly). All thanks to the powers of compound interest. Far from paying it off, you will increase the amount you owe. If nothing remains unchanged, you will never get out of it. One has to wonder that it is not by chance that minimum payments are offered below the monthly compound interest. Even when presented with all the financial jargon and figures, 99.9% of credit card users will not understand the implications until they confront their card statements.

If you find yourself in this situation you need to take action either by increasing your minimum monthly payments over the monthly compound interest (slow pay-off process and you will pay a significant amount in interest), shifting the debt to a cheaper credit card deal, cancelling it out by taking a personal loan or paying it off with savings. Do not just ignore it. It will not go away.

No wonder why credit cards are in such wide offer in every possible colour and format, for every age group, credit score profile and introductory period. Credit card companies are dying for your custom. They want you to get in debt. The debt business is just an obscenely profitable business. Fortunately, there is a way to take advantage of credit card debt and make free money out of it. I will be most glad to show it to you. Stay tuned.